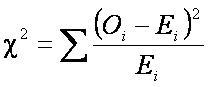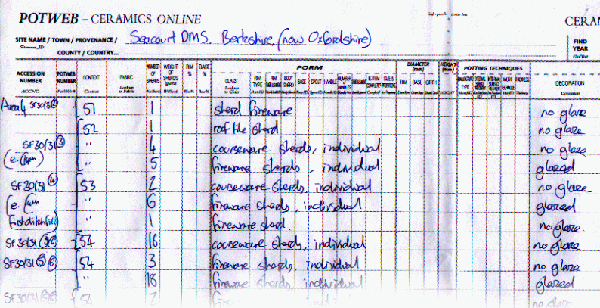
The first task was to count the number of potsherds from each area and record in detail the fabric and decoration. To keep things simple, the potsherds were divided into either fineware or coarseware, glazed or unglazed and recorded on paper on relevant forms (See Figure 5. below).

Figure 5. A typical ceramics recording form

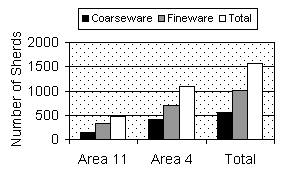
Results were then entered into a spreadsheet program; in this case Microsoft Excel was used. When dealing with a large amount of individual records (1,573 individual sherds for this project) a spreadsheet package is the best means of manipulating the data to produce clear and informative results. 'right-click' here to download and save the Excel Worksheet. Table 1. (see below) summarises the total observed coarseware and fineware sherds from each area.

Once the data has been recorded, the process of extracting information can begin. In this case, a visual interpretation of the data, by means of a bar graph (see above), suggests that the ratio between coarseware and fineware sherds differs only slightly between the two areas. However, the modern day archaeologist can turn to the field of statistics in order to obtain a mathematical analysis.

There is a significance test that sums up the entire comparison in a single probability value. It is the chi-square test, named after the statistic it produces, represented by the Greek letter chi.

where:

  = the observed value for the ith cell of the table;

 = the expected value for the ith cell of the table.

The following table of expected values is based upon the average proportions of total coarseware and fineware sherds across the two areas.

Table 2. Expected Number of Sherds of

Different Fabrics from Area 11 and Area 4

The Chi-square test is designed to answer the question:

 "How likely is it that we could select samples with proportions of coarseware and fineware sherds as different as these if the two areas did not really differ in regard to coarseware and fineware proportions?"

By constructing a table of expected values (Table 2.) and comparing this to the observed values (Table 1.), we can produce a value for chi-square, which in turn can be looked up in a chi-sqaure distribution table (Arkin and Colton, 1963: Table 14.) to produce a statistic.

In our case, the answer to the question turns out to be that there is somewhere between a 5% and a 2% risk that we could select samples as different as these if the two areas did not really differ in regard to coarseware and fineware sherd proportions.